Question

(1) The scores on an aptitude test for finger dexterity are normally distributed with mean 250 andstandard deviation 65.a What is the probability that a person selected at random will score between 240 and 270 on thetest?b) Test is given to a random sample of seven people. What is the probability that the mean score,I for the sample will be between 240 and 270?

Answer 1

We know that the mean and standard deviation of the dexterity test are 250 and 65 respectively; that is we have that:

`\begin{gathered} \mu=250 \\ \sigma=65 \end{gathered}`

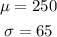
We also know that the scores are normally distributed. With this in mind.

a.

We want the probability:

`P(240to get it, we need to find the z-score for each limit. The z-score is given by:[tex]z=(x-\mu)/(\sigma)`

Then, we have that:

Then, in this case, we have that:

`\begin{gathered} \bar{x}=250 \\ \sigma_{\bar{x}}=\frac{65}{\sqrt[]{7}}=24.568 \end{gathered}`

Now, we want to know the probability:

`P(240<\bar{x}<270)`

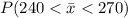
To find it we need to find the z-value, which is given by:

`z=\frac{\bar{x}-\mu}{\sigma_{\bar{x}}}`

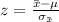
Applying it to the probability we have that:

[tex]\begin{gathered} P(240<\bar{x}<270)=P(\frac{240-250}{24.568}Therefore, the probability that the mean score of the sample lies between 240 and 270 is 0.4503