Question

A table of values of a linear function is shown below

Answer 1

• slope: 3

,

• y-intercept: 6

,

• equation: y = 3x + 6

Step-by-step explanation

The slope-intercept form of the equation of a line is,

`y=mx+b`

Where m is the slope and b is the y-intercept.

The slope of a line passing through points (x₁, y₁) and (x₂, y₂) is,

`m=(y_1-y_2)/(x_1-x_2)`

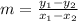
In this case, to find the slope we have to take two pairs of values from the table. Using the points (1, 9) and (0, 6) we have,

`m=(9-6)/(1-0)=(3)/(1)=3`

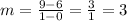
Hence, the slope is 3.

The y-intercept is the value of y where the line intersects the y-axis. This always occurs at x = 0, so the y-intercept is shown in the table as the value of y for x = 0,

Hence, the y-intercept is 6.

Finally, we have to substitute m and b with the slope and y-intercept found to write the equation for this function. Hence, the equation is y = 3x + 6.