a)
We know that the angular acceleration is related to the linear acceleration by:
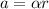
where alpha is the angular acceleation and r is the radius, then, in this case we have:
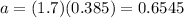
Therefore the linear acceleration is 0.6545 meters per second per second.
b)
The linear velocity is related to the angular velocity by:
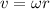
where omega is the angular velocity, plugging the values we have and solving for the angular velocity we have:
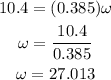
Therefore the angular velocity is 27.013 radians per second.
c)
To determine the time it takes for the cyclist to reach that velocity we use the equation:
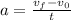
since he started at rest this means that the initial velocity is zero; plugging the values we know and solving for t we have:
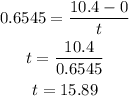
Hence it takes 15.89 seconds to reach this velocity. To determine how many radians the wheels turned we use the fact that:
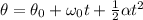
then we have:
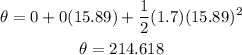
Therefore the wheels turned 214.618 radians.
d)
To determine how far the bycicle traveled in this time we use:
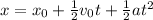
then we have:

Therefore the bicycle traveled 82.628 meters.