Answer:
x-2y=-6.
Step-by-step explanation:
Given a line with a slope of 1/2 that passes through the point (2,4):
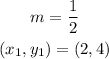
Substitute these into the point-slope form of the equation of a line:
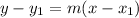
This gives:
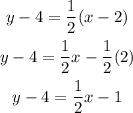
We can simplify further:
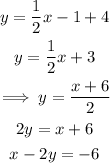
The equation of the line is x-2y=-6.