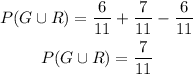Answer:
7/11
Step-by-step explanation:
Given;
Total number of marbles = 11
Number of marbles with red on them = 7
Number of marbles with blue on them = 4
Number of marbles with green on them = 6
Number of marbles with red and green on them = 6
We'll use the below formula to determine the probability that a randomly chosen marble has either green or red on it;
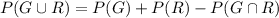
where;

Let's go ahead and substitute the above values into the formula and evaluate;