Question

The graph of g(x) is obtained by reflecting the graph of f(x) = 4 Ixl over the x-axis. = Which equation describes g(x)? O g(x) = -4 Ixl O g(x) = lx – 41 = O g(x) = lxl - 4 - g(x) = (x + 41 =

Answer 1

To answer this question, we need to remember that if we have the function f(x), the function -f(x) is the reflection of the function f(x) in the x-axis.

Then, the graph of the function g(x) is the same as g(x) = -f(x). Then, we have that:

`g(x)=-f(x)\Rightarrow f(x)=4|x|\Rightarrow-f(x)=-4|x|`

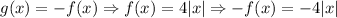
Then

`g(x)=-4|x|`

We can check this graphically as follows (the red graph is the function f(x) = 4|x| and the blue function is g(x) = -4|x|):

Therefore, g(x) = -4|x| is the reflection of the function f(x) = 4|x| over the x-axis.

In summary, the equation that describes g(x) is:

`g(x)=-4|x|`

(First option).