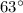Question

the measure of two consecutive angles in a parallelogram are in a 13:7 ratio. What is the measure of the acute angle in the parallelogram

Answer 1

In a parallelogram, consecutive angles are supplementary angles.

Let a and b be two consecutive angles in a parallelogram, so that their ratio is 13:7. Then:

`(a)/(b)=(13)/(7)`

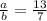
Since they are supplementary angles, then:

`a+b=180`

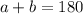
Isolate a from the first equation and substitute the expression for a in the second equation:

`\begin{gathered} a=(13)/(7)b \\ (13)/(7)b+b=180 \\ \Rightarrow(20)/(7)b=180 \\ \Rightarrow b=(7)/(20)*180 \\ \Rightarrow b=63 \end{gathered}`

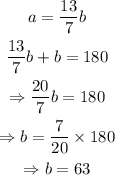
The value of a can be calculated from any of the equations from the value of b, and turns out to be equal to 117.

From the angles 117° and 63°, the acute angle is 63°.

Therefore, the measure of the acute angle in the parallelogram, is:

`63^(\circ)`