Question

11=Circumference and area of a circleFind the area and the circumference of a circle with diameter 7 yd.Use the value 3.14 for Ti, and do not round your answers. Be sure to include the correct units in your answers.ydydyouArea:7 yd0Circumference:х?ExplanationCheck2021 MG HER ARC

Answer 1

The diameter of the circumference is 7 yd. Its radius is half the diameter, then:

`\begin{gathered} r=(7)/(2)yd \\ \\ r=3.5yd \end{gathered}`

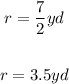
The area of a circle is given by the following formula:

`A=\pi\cdot r^2`

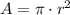
Where r is the radius, 3.5 yd in this case. We can replace the values and calculate it now:

`\begin{gathered} A=3.14\cdot(3.5yd)^2 \\ A=3.14\cdot12.25yd^2 \\ A=38.465yd^2 \end{gathered}`

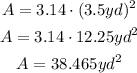
The area of the circle is 38.465 square yards.

To calculate the circumference we use the following formula:

`C=2\cdot\pi\cdot r`

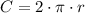
Again, we just need to replace the values:

`\begin{gathered} C=2\cdot3.14\cdot3.5yd \\ \\ C=6.28\cdot3.5yd \\ \\ C=21.98yd \end{gathered}`

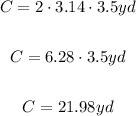
The circumference of the circle is 21.98 yards.