Question

How Much Paint Would Cover This Pyramid Without The Square Base ?

Answer 1

To answer this question, we will assume that the pyramid's slant height is 10ft.

We have a square pyramid in which we have:

• The pyramid's base is a square with a side that measures 6ft.

,

• The height of the pyramid is equal to 8ft.

,

• The slant height is 10ft

Then we need to find the surface area of the pyramid without the square base, and we can see that:

1. We can see that the surface area of the pyramid without the square base is represented by four (4) triangles with equal base (6ft) and equal height (10ft). Then since the area of a triangle is given by:

`A___(triangle)=(bh)/(2)`

2. Therefore, we need to find the area of one of the triangles, and then multiply this result by 4 to find the asked area as follows:

`A_(triangle)=(6ft*10ft)/(2)=(60ft^2)/(2)=30ft^2`

3. Then the total area of the pyramid without the square base is:

`\begin{gathered} A_(4triangles)=4(30ft^2)=120ft^2 \\ \\ A_(4triangles)=120ft^2 \end{gathered}`

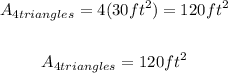
Therefore, in summary, the paint would cover 120ft² (square feet) without the square base.