SOLUTION
Write out the equation
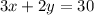
The equation of a line in slope intercept form is given by
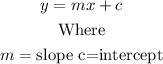
Hence
From the equation given, we make y the subject of the formula of the equation given.
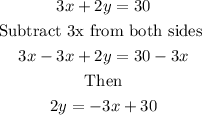
Divide both sides by 2
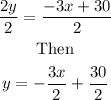
Hence
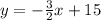
Therefore
The equation of the line in slope intercept form is
y=-3/2x + 15