For the first prize, we have a box with four names on it. Frank, Sofia, Eldridge and Jake. The probability of drawing a name is the same for any of the names.
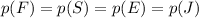
When we have a set with a finite amount of elements, the probability of randomly selecting an specific type of element from this set is given by the ratio between the amount of elements with this specific type by the total amount of elements in the set.
Using this definition, the probability of selecting a specific name from the box is given by the total amount of this name(since they're all unique, there's only one Jake, one Frank, and so on) by the total amount of names. The probabilities are
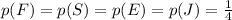
Those are the probabilities for the first drawn. Since the names are replaced for the second drawn, the total amount of names and the amount of each name stays the same, therefore, the probabilities stays the same for the second drawn.
item (a):
Someone is going to win on the first drawn and the probability for the same person to win on the second drawn is also 1/4, therefore, the probability for someone to win both prizes is 1/4.
item (b):
It was stated on the previous item that the probability for the same person to win on the second drawn is also 1/4. The sum of the probabilities for all outcomes of an event must add up to 1. 1 minus the probability for the same person to win on the second drawn will give to us the probability for a different person to win on the second drawn.
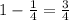
Then, the probability of having two different winners is 3/4.
item(c):
the probability of Sofia winning on the first drawn is 1/4, and the probability for her to win on the second drawn is also 1/4. Each drawn is an independent event. The probability of independent events happening simultaneously is given by the product of the probabilities of each drawn.
She can win the first prize and not win the second, win the second prize and not win the first, and she can win both of them. The sum of those three probabilities are our answer. The probability that she wins the first prize but not the second is

The probability that she wins the second prize but not the first is

And the probability that she will win both of them is
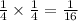
The sum of those probabilities is
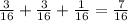
The probability that Sofia will win at least one prize is 7/16.
item (d):
As it was stated before, the probability of Sofia winning on the first drawn is 1/4, and the probability for her to win on the second drawn is also 1/4. For Frank, we have the same values, therefore, the probability that he is going to win both prizes is
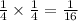
The probability that Frank is going to win both prizes is 1/16.
item (e):
On this item, we have two scenarios. Jake wins the first prize and Eldridge wins the second prize, or the other way around.
The probability that Jake will win the first prize is p(J) = 1/4, and the probability that Eldridge wins the second prize is p(E) = 1/4. To both events to happen, we have
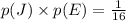
Since the other way around has the same probability, the probability that Jake and Eldridge will be the winners is
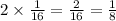
the probability that Jake and Eldridge will be the winners is 1/8.