Binomial expansion

The coefficient of each term is:
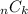
That is, the number of combinations of k objects from a set with n objects
In the binomial:
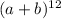
the value of n is n = 12. In the fourth term, k = 3 (remember that k starts at zero). Therefore, the coefficient of the 4th term is:
