Question

How can I find the equation of a circle with the coordinates (4,6)Center = (4,6), Diameter = 3 ft

Answer 1

a) We have to find the equation of a circle with center c = (4,6) and diameter D = 3 ft.

We can express a circle with center (a,b) and radius r as:

`(x-a)^2+(y-b)^2=r^2`

Then, in this case, r = D/2 = 1.5, so we can write the equation as:

`\begin{gathered} (x-4)^2+(y-6)^2=1.5^2 \\ x-4)^2+(y-6)^2=2.25 \end{gathered}`

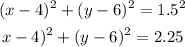
b) We now have to place another circle with its center 7 ft to the right and 2 ft up from the previous sprinkle.

Its radius, due to the increase in the preasure, will be two times the radius of the previous cicrle. Then, for this circle, r = 1.5*2 = 3 ft.

We can calculate the new center as:

`\begin{gathered} x_c=4+7=11 \\ y_c=6+2=8 \end{gathered}`

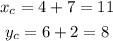
With a center of (11, 8) and radius r = 3, the circle can be expressed as:

`\begin{gathered} (x-11)^2+(y-8)^2=3^2 \\ (x-11)^2+(y-8)^2=9 \end{gathered}`

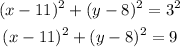
We can graph both circles as:

Answer:

a) (x - 4)² + (y - 6)² = 2.25

b) (x - 11)² + (y - 8)² = 9