Answer:
m = -2
Step-by-step explanation:
The given function is:

For x - 2 to be a factor of f(x):
f(x) must be equal to zero when x = 2
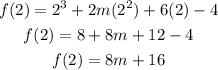
Let f(2) = 0 to solve for m
8m + 16 = 0
8m = -16
m = -16/8
m = -2
Therefore, for x - 2 to be a factor of x^3 + 2mx^2 +6x -4, the value of m is -2