Question

A pure silver lions fan throws a roll of toilet paper at 7.2 m/s from her seat at Ford‘s field during a recent game. how fast is the 0.4 KG roll going when it strikes an opposition player 16. 1 m below?

Answer 1

Given:

The mass of the roll is m =0.4 kg.

The velocity of the roll is v = 7.2 m/s at a height h = 16.1 m.

To find the velocity when it strikes the opposition player, where height h'= 0 m

Step-by-step explanation:

According to the law of conservation of energy, the total energy is always conserved, so

`\begin{gathered} (P\mathrm{}E\mathrm{})_h+(K\mathrm{}E.)_h=(P.E.)_(h^(\prime))+(K.E.)_(h^(\prime)) \\ mgh+(1)/(2)mv^2=mgh^(\prime)+(1)/(2)mv^(\prime2) \end{gathered}`

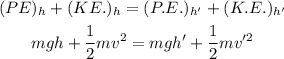
Here, g = 9.8 m/s^2 is the acceleration due to gravity.

On substituting the values, the velocity will be

`\begin{gathered} 0.4*9.8*16.1+(1)/(2)*0.4*(7.2)^2=0.4*9.8*0+(1)/(2)*0.4v^(\prime2) \\ 63.112+10.368=0+0.2v^(\prime2) \\ v^(\prime)=19.17\text{ m/s} \end{gathered}`

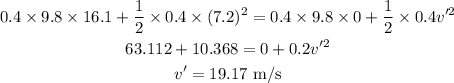
Final Answer: The velocity of the roll when it strikes the player is 19.17 m/s