Question

Question a b c, need help to to solve them...

Answer 1

infinityAnswer:

p(0) = 20

p(5) = 59

Horizontal Asymptote: y = 2400 as t approaches infinity

Explanation:

part C.

To find the horizontal asymptote, we investigate the behaviour of the function p(t) as t approaches infinity.

Now as t approaches inifinty

`P(t)=(60(1+0.4t))/(0.01t+3)`

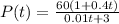
the terms 0.04 t and 0.01t become extremely large; so large in fact that we can ignore constant 3 and 1 to get

`P(t)\approx(60\cdot0.4t)/(0.01t)`
`P(t)\approx2400`

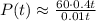
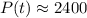
which means at t -> ∞, p(t) = 2400. In the context of insect population this means that if we wait a long enough time, eventually the insect population will stop decreasing and approach 2400. In other words, the population limit is 2400 insects