ANSWER:
122 gallons
Explanation:
We have the following function:
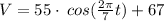
The first thing is to calculate the periodicity of the function. The value of the periodicity would be the value of x (in this case t) to calculate the value of y, that is, in this case the volume.
As follows:
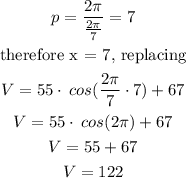
Therefore the maximum volume would be 122 gallons.