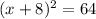First step is to separate the terms with variables from the constant terms.
Add 13 to both sides of the equation :
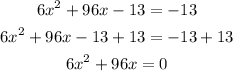
Divide both sides by 6 :

Next step, completing the square by adding this term to both sides of the equation :
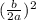
From the equation,
a = 1
b = 16
So it follows that :
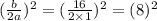
Adding this to both sides of the equation :
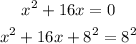
And you will get a perfect square trinomial on the left side of the equation in the form :
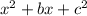
It can be factored as :
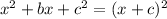
So the equation will be :
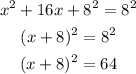
The answer is :