For a)
x=2
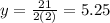
x=5
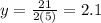
b)
c)
We locate for each case the points
d)
First we need to solve the equation given
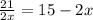
We isolate the x
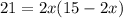
we simplify
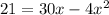
Then we make zero the equation
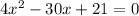
Then we solve the second-degree equation.
The solutions are
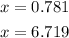
Both solutions are inside the given interval
Therefore the lines are