This is an inverse proportionality question, and the relationship between the number of people (say, n) and the cost per person (say, c) can be written as:

Step 1: Now, we introduce a constant of proportionality as follows:
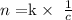
Step 2: Now, we solve to obtain the value of the constant of proportionality, as follows:
We are given that, originally, there were 12 people and the cost per person was $20.
The above means that, when:
n = 12 , c = $ 20
Now, we substitute for n and c in the proportionality equation as follows:
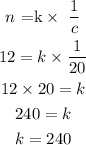
Thus, the constant of proportionality is k = 240
Step 3: Now, we can find the new cost per person (c) if the number of people changed to 3, as follows:
From the proprtionality equation, given as:
![undefined]()