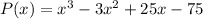Question

Find a polynomial function of lowest degree with rational coefficients

Answer 1

Since -5i is a zero, then its complex conjugate +5i is also a zero of the function.

Therefore,

x + 5i, x - 5i , and x - 3 are factors of the polynomial.

Hence, the polynomial function, P(x), of the lowest degree with rational coefficients​ is given by

`P(x)=(x+5i)(x-5i)(x-3)`

Which implies that

`\begin{gathered} P(x)=(x^2-(5i)^2)(x-3)=(x^2-25i^2)(x-3) \\ \text{ Since i}^2=-1,\text{ then we have} \\ P(x)=(x-3)((x^2+25)=x^3+25x-3x^2-75 \end{gathered}`

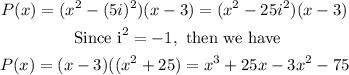
Hence the polynomial is

`P(x)=x^3-3x^2+25x-75`