Notice that angle z and the angle with measure 70⁰ is a linear pair. Hence, it follows that they are supplementary (they'll sum up to 180⁰):
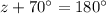
Solve for z in the equation:
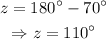
Using the Angles formed by two intersecting chords theorem: If two chords intersect inside a circle, then the measure of the angle formed is one-half the sum of the measure of the arcs intercepted by the angle and its vertical angle , it follows that:
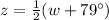
Substitute z=110⁰ into the equation and solve for w:
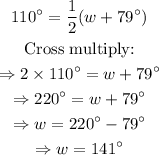
The value of w is 141.