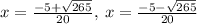You have to see if the polynomial is factorable
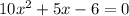
In this case, it isn't, so now see the grade of the polynomial, we can see that is grade 2, so we can use the quadratic formula to find the roots:
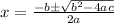
the polynomial is in the form:
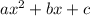
So, replace
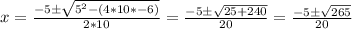
So we have two imaginary roots