Question

7/8 +9/10 write your answer as a fraction in simplest form

Answer 1

Adding Fractions

We are required to find the sum:

`(7)/(8)+(9)/(10)`

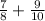
In order to be able to find the sum, we first need to make both denominators with the same value, or a common denominator.

The procedure is called Least Common Multiple of the denominators and consists of finding the lowest multiple of both denominators, in this case:

LCM(8,10)

To find the LCM, we write the prime divisors of each number as follows:

8 = 2*2*2

10 = 2*5

Now we select all the divisors the maximum number of times they appear, that is:

LCM = 2*2*2*5 = 40

Now we divide the LCM by each denominator and multiply the result by each numerator:

`(7)/(8)+(9)/(10)=(5\cdot7)/(40)+(4\cdot9)/(40)`
`(7)/(8)+(9)/(10)=(35)/(40)+(36)/(40)`

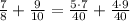
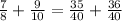
Operating:

`(7)/(8)+(9)/(10)=(35+36)/(40)=(71)/(40)`

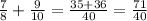
The result is 71/40