Question

How does the slope off(x) relate to the slope off-1(x)

Answer 1

Answer:

The slope of f(x) is inverse of the slope of f^-1(x)

Step-by-step explanation:

The given function is:

`f(x)=(3)/(4)x-5`

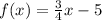
The function is of the form f(x) = mx + c

where m is the slope

Comparing f(x) =(3/4)x - 5 and f(x) = mx + c:

The slope, m = 3/4

The slope of f(x) = 3/4

The inverse of f(x) is calculated below

`\begin{gathered} f(x)=(3)/(4)x-5 \\ (3)/(4)x=f(x)+5 \\ 3x=4(f(x))+20 \\ x=(4)/(3)f(x)+(20)/(3) \\ f^(-1)(x)=(4)/(3)x+(20)/(3) \end{gathered}`

The slope of f^-1(x) = 4/3

Note that 3/4 and 4/3 are inverse of each other

Therefore, the slope of f(x) is inverse of the slope of f^-1(x)