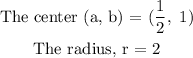Answer:
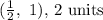
Explanations:
The given equation is:
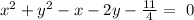
The standard equation of a circle is given as:
(x - a)² + (y - b)² = r²
where (a, b) is the center
r is the radius
Express the given equation in form of the standard equation
Collect like terms
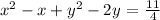
Add the squares of the half of the coefficients of x and y to both sides of the equation
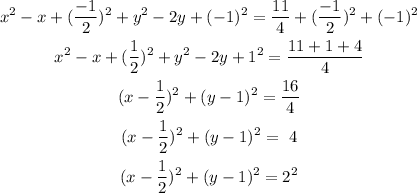
Compare the resulting equation with (x - a)² + (y - b)² = r²