Question

24) A high school had 1200 students enrolled in 2003 and 1500 students in 2006. If the student population, p, grows as a linear function of time t, where t is the number of years after 2003. Part B: Find a linear function that relates the student population to the time.

Answer 1

The population of the student is a linear function with respect to time.

Let population be "p" and time be "t", thus we can write general form of the equation as:

`p=mt+b`

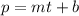
Where

m is the slope

b is the y-intercept

of the line...

Let's take the year 2003 at t = 0.

So,

2004 would be t = 1

2005 would be t = 2

2006 woud be t = 3

We have population of 1200 at the base year 2003, thus a coordinate pair of point (t, p) will be (0, 1200).

We have a population of 1500 in 2006, thus a coordinate pair of point (t, p) will be (3, 1500).

We have two points:

(0, 1200)

(3, 1500)

Let's calculate the slope, which is the rate of change of p with respect to t.

Change in p = 1500 - 1200 = 300

Change in t = 3 - 0 = 3

Rate of Change = 300/3 = 100

This is the slope, or m.

Thus, the equation will be:

`p=100t+b`

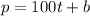
To find b, we can use the point (t,p) = (0, 1200). So,

`\begin{gathered} p=100t+b \\ 1200=100(0)+b \\ b=1200 \end{gathered}`

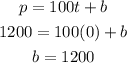
The correct equation will be:

`p=100t+1200`

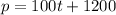
Matching with answer choices, it is First Option, f(x) = 100x + 1200