We can use the simple interest formula to solve this problem. Our working equation is
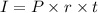
where P is the principal amount, r is the interest rate, and t is the time. If we assume that the rate of this problem grows every year, we need to convert the time into years. There are 365 days in a year. Hence, to convert 100 days into years, we have
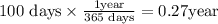
Substitute the given on the given working equation and solve, we get

Answer: 162