In order to find the area of the dark triangle (let's call it 'x'), we need to calculate the area of the whole rectangle and the area of the three small triangles.
The area of the rectangle is:
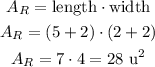
The area of each triangle is:
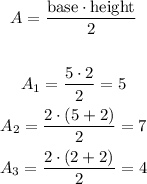
Now, using the additivity principle, we have that:
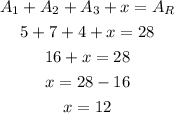
So the area of the dark triangle is equal 12 square units.