ANSWER
• Parallelogram Area = 72 cm²
,
• Triangle Area = 24 cm²
,
• Area of composite figure = 96 cm²
Step-by-step explanation
The area of a parallelogram is the product between the length of the base and the height of the parallelogram,
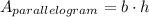
In this case, b = 12cm and h = 6cm,
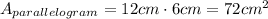
The area of a triangle of base b and height h is,
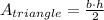
In this case, b = 12cm and h = 4cm,
![A_(triangle)=\frac{12\operatorname{cm}\cdot4\operatorname{cm}}{2}=(48cm^2)/(2)=24cm^2]()
The area of the composite figure is the sum of the areas of the two figures,
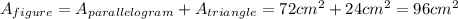
The total area of the composite figure is 96 cm²