Question

The terminal of 0 is (1/2,3/2). What is the cos 0?

Answer 1

Option B

Step-by-step explanation:

Given that:

`\text{Terminal point of }\theta=((1)/(2),\frac{\sqrt[]{3}}{2})`

If P(x, y) is the terminal point of an angle, then x is the length of its adjacent side and y is the length of its opposite side.

Here,

`\begin{gathered} \text{Length of adjacent side =}(1)/(2) \\ \text{Length of opposite side =}\frac{\sqrt[]{3}}{2} \end{gathered}`

First, find the length of hypotenuse using the Pythagorean theorem.

`\begin{gathered} \text{Hypotenuse}^2=Adjacentside^2+Oppositeside^2 \\ =((1)/(2))^2+(\frac{\sqrt[]{3}}{2})^2 \\ =(1)/(4)+(3)/(4) \\ =1 \\ \text{Hypotenuse}=\sqrt[]{1}=1 \end{gathered}`

Using the trigonometric ratio,

`cos\theta=\frac{\text{Adjacent side}}{Hypotenuse}`

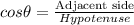
Plug the values into the formula.

`\begin{gathered} cos\theta=((1)/(2))/(1) \\ =(1)/(2) \end{gathered}`

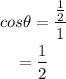
Hence, option B is correct.