Solution:
Given the table;
The graph of the points is;
(a) The logarithm model for the data using the first and last data points in the table is;

(b)
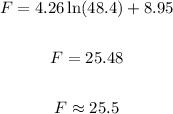
Thus, the difference between the model value and the observed value is approximately 1.2. The model predicts a frequency of 25.5 as compared to the observed frequency of 25.3
(c)
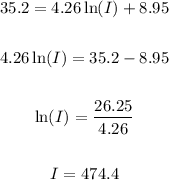
Thus, the difference between the model intensity and the observed value is approximately 37.1. And that is quite a wide difference. The model predicts an intensity of 474.4 as compared to the observed intensity of 437.3