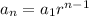Solution
Explanation:
We are to write the first five terms of a sequence, along with the explicit and recursive formula for the general term of the sequence.
Let the first five terms of a sequence be 5, 10, 20, 40 and 80
These terms are taken from a geometric sequence with first term

first term a = 5
common ratio r = 2
Therefore, we have
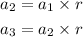
Therefore, the recursive formula is
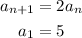
And explicit formula is