The drawing of a right triangle inscribed in a circle is shown below:
AD and BD are the legs of the triangle and AB is the hypotenuse, which coincides with the diameter of the circle centered at C.
The legs of the triangle measure 7 meters and 3 meters, so we can find the hypotenuse as follows:
![AB=\sqrt[]{7^2+3^2}](https://img.qammunity.org/2023/formulas/mathematics/college/s53gsdiqxler5qx7z3we0i6ij69z94suo9.png)
We have applied the Pythagorean Theorem. Calculating:
![\begin{gathered} AB=\sqrt[]{49+9}=\sqrt[]{58} \\ AB\approx7.62m \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/m013h1fuh4r5f5ln7251cmrslr7le8x6dl.png)
The circumference of a circle is the diameter times pi:
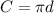
Substituting the value of AB (diameter):
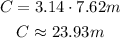
Rounding to the nearest whole number, the circumference is 24 meters.