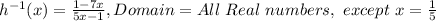Question

I need help with this math problem because I am having a hard time understanding the problem and finding the answer. Can u help me

Answer 1

`h(x)=(x+1)/(5x+7),Domain=All\text{ }Real\text{ }numbers,\text{ }except\text{ }x=-(3)/(2)\text{ }and\text{ }x=-(7)/(5)`
`h^(-1)(x)=(1-7x)/(5x-1),Domain=All\text{ }Real\text{ }numbers,\text{ }except\text{ }x=(1)/(5)`

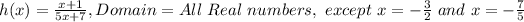
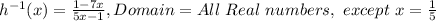
Step-by-step explanation:

The notation for composition of functions is:

`(f\circ g)(x)=f(g(x))`

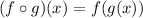
In this case:

`\begin{cases}f(x)={(x)/(x+2)} \\ g(x)={(x+1)/(2x+3)}\end{cases}`

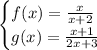
To do the composition, we replace the x in the f(x) with the function g(x):

`(f\circ g)(x)=f(g(x))=(g(x))/(g(x)+3)=((x+1)/(2x+3))/((x+1)/(2x+3)+2)`

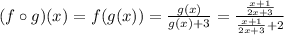
And solve:

`=((x+1)/(2x+3))/((x+1)/(2x+3)+2)=((x+1)/(2x+3))/((x+1)/(2x+3)+(2(2x+3))/(2x+3))=((x+1)/(2x+3))/((5x+7)/(2x+3))=((x+1)(2x+3))/((2x+3)(5x+7))`

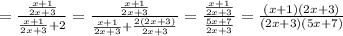
Here, we can calcualte the domain. The function is not defined when teh denominator is 0, thus:

`2x+3=0\Rightarrow x=-(3)/(2)`
`5x+7=0\Rightarrow x=-(7)/(5)`

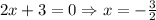
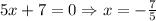
Since the function can't be evaluated when x = -3/2, we can cancel the terms (2x+3) in the numerator and denominator:

`((x+1)(2x+3))/((2x+3)(5x+7))=(x+1)/(5x+7)`

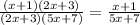
Thus:

`\begin{equation*} h(x)=(x+1)/(5x+7),Domain=All\text{ }Real\text{ }numbers,\text{ }except\text{ }x=-(3)/(2)\text{ }and\text{ }x=-(7)/(5) \end{equation*}`

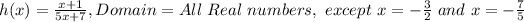
Now, to find the inverse of the function, we first switch the variables:

`y=(x+1)/(5x+7)\Rightarrow x=(y+1)/(5y+7)`

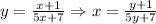
And solve for y:

`\begin{gathered} \begin{equation*} x=(y+1)/(5y+7) \end{equation*} \\ . \\ x(5y+7)=y+1 \\ . \\ 5xy+7x=y+1 \\ . \\ 5xy-y=1-7x \\ . \\ y(5x-1)=1-7x \\ . \\ y=(1-7x)/(5x-1)\Rightarrow h^(-1)(x)=(1-7x)/(5x-1) \end{gathered}`

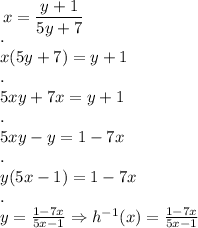
And since the denominator can't be 0:

`5x-1=0\Rightarrow x=(1)/(5)`

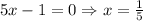
Thus:

`\begin{equation*} h^(-1)(x)=(1-7x)/(5x-1),Domain=All\text{ }Real\text{ }numbers,\text{ }except\text{ }x=(1)/(5) \end{equation*}`