ANSWER
x = 20
Step-by-step explanation
To solve this equation, first, we have to subtract 11 from both sides,
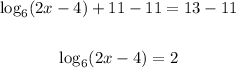
Then, there is the property of logarithms that states that if we raise the base of a logarithmic expression to the expression, the result is the argument of the logarithm,
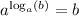
So, the next step is to raise 6 to each side of the equation,
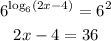
Then, add 4 to both sides,
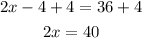
And divide both sides by 2,
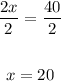
Hence, the solution is x = 20.