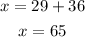Question

Find two positive numbers whose difference is 29 and whose product is 2340.

Answer 1

The numbers are 65 and 36

Explanation:

From the statement we can propose the following system of equations:

`\begin{gathered} x-y=29\rightarrow x=29+y\text{ (1)} \\ x\cdot y=2340\text{ (2)} \end{gathered}`

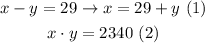
We replace equation (1) in equation (2), and solve for y, like this:

`\begin{gathered} (29+y)\cdot y=2340 \\ y^2+29y=2340 \\ y^2+29y-2340=0 \\ (y-36)\cdot(y+65)=0 \\ y-36=0\rightarrow y=36 \\ y+65=0\rightarrow y=-65 \end{gathered}`

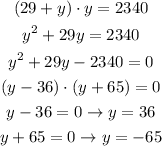
Since it must be a positive number, one of the two numbers is 36. And the other would be:

`\begin{gathered} x=29+36 \\ x=65 \end{gathered}`