A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value. Its general term is
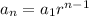
The value r is called the common ratio.
On the sequence of our problem, we know the second and fifth term. If we substitute those values on the general term presented, we have
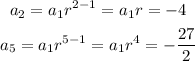
If we divide the fifth term by the second term, we're going to have
![(a_5)/(a_2)=(a_1r^4)/(a_1r)=r^3\operatorname{\implies}r^3=((-27\/2))/((-4))]()
Solving for r, we have
![\begin{gathered} r^3=((-27\/2))/((-4)) \\ r^3=(27)/(8) \\ r=\sqrt[3]{(27)/(8)} \\ r=(3)/(2) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/86buo82vb3bca0n2sqgumkh66ro8b5j9u1.png)
The common ratio is 3/2.