Question

I was a little confused on what to do or where to start, could you help?

Answer 1

Our approach is to determine the equation of the function and when we do, we can substitute as appropriate.

`\begin{gathered} \text{ At x = 4, y = 12} \\ (y)/(x)=(12)/(4)=3 \\ y=3x \end{gathered}`

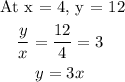
Now we have established a relationship between x and y.

`\begin{gathered} \text{ When y = 6,} \\ 6=3x \\ \text{ Divide both sides by 3 to get:} \\ x=2 \end{gathered}`

`\begin{gathered} \text{ When x = 6,} \\ y=3(6)=18 \\ y=18 \end{gathered}`

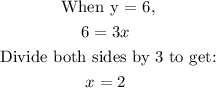
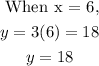
We can confirm these values by tracing downwards to 2 when y = 6

In the same way, we can trace leftward to 18 when x = 6