Question

Use the vertex (h, k) and a point on the graph (x, y) to find the general form of the equation of the quadratic function.(h, k) = (−3, −1), (x, y) = (−5, 3)

Answer 1

y = x² + 6x +8

Explanation:

The equation in its vertex form has the following form:

`\begin{gathered} y=a(x-h)^2+k \\ \\ \text{ where \lparen h, k\rparen is the vertex } \end{gathered}`

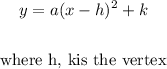
We solve for a which is the coefficient of the principal of the equation as follows:

`a=(y-k)/((x-h)^2)`

We substitute each value to be able to determine the value of a, like this:

`a=(3-(-1))/((-5-(-3))^2)=(3+1)/((-5+3)^2)=(4)/(2^2)=1`

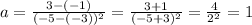
Now we calculate education in its vertex form:

`\begin{gathered} y=1\cdot(x-(-3))^2-1 \\ \\ y=(x+3)^2-1 \\ \\ \text{ We solve to obtain it in its general form, like this:} \\ \\ y=x^2+6x+9-1 \\ \\ y=x^2+6x+8 \end{gathered}`

The general form of the equation of the quadratic function is y = x² + 6x +8