Find the perimeter of the polygon with the vertices UC - 2, 4), V(3, 4), and W(3– 4). Round your answer to the nearest hundredth. The perimeter is about units.

Question

asked Apr 12, 2023 70.4k views

1 Answer

Sadeghbayan · Answer 1 · 2023-04-19T10:03:43+0000

Given the polygon of the vertices :

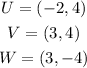
$\begin{gathered} U=(-2,4) \\ V=(3,4) \\ W=(3,-4) \end{gathered}$

The graph of the points and the polygon is as shown in the following graph :

Using the graph to find the distance between the points :

So, UV = 5

And VW = 8

The distance between the points U and W will be calculated using Pythagorean :

$UW=\sqrt[]{5^2+8^2}=\sqrt[]{25+64}=\sqrt[]{89}\approx9.43$

So, the perimeter of the polygon =

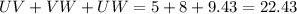
So, the answer is : 22.43 ( to the nearest hundredth )

So, The perimeter is about 22.43 units.