Question

Determine whether figure ABCD is a parallelogram (let me know if you need to see the answer choices)

Answer 1

Figure ABCD is a parallelogram

AB is congruent to CD, and the slopes of AB and CD are the same, so one pair of opposite sides AB and CD are both parallel and congruent.

Step-by-step explanation:

For any quadrilateral to be considered a parallelogram, one pair of opposite sides of the quadrilateral must be parallel and congruent.

We can see from the graph that the vertices of figure ABCD are A(1, 2), B(3, 4), C(3, -1), and D(1, -3)

Let's go ahead and determine the slope of line AB using the slope formula;

`\text{Slope of line AB }=(y_2-y_1)/(x_2-x_1)=(4-2)/(3-1)=(2)/(2)=1`

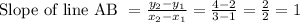
Let's determine the slope of line CD using the slope formula as seen below;

`\text{Slope of line CD }=(y_2-y_1)/(x_2-x_1)=(-3-(-1))/(1-3)=(-3+1)/(-2)=(-2)/(-2)=1`

We can see that the slopes of line AB and CD are the same, therefore both lines are parallel since parallel lines always have the same slope.

Let's determine the distance of line AB using the distance formula;

`\begin{gathered} \text{Distance of AB }=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(3-1)^2+(4-2)^2} \\ =\sqrt[]{4+4^{}^{}} \\ =\sqrt[]{8} \\ =2\sqrt[]{2} \end{gathered}`

Let's determine the distance of line CD using the distance formula;

`\begin{gathered} \text{Distance of CD = }=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\sqrt[]{(1-3)^2+(-3+1)^2_{}} \\ =\sqrt[]{4^{}+4} \\ =\sqrt[]{8} \\ =2\sqrt[]{2} \end{gathered}`

We can see that the length of lines AB and CD are the same.

We can see from the above that one pair of opposite sides of the quadrilateral, AB and CD, are parallel and congruent, therefore we can say that figure ABCD is a parallelogram.