From the question given, we have the following information;

In order to determine the probability that the next customer would be a credit card customer, we shall calculate as follows;
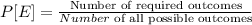
Using the details we are given, the probability that the next customer would be using a credit card would be;

Next, we are told that next week, 600 customers are expected. Therefore, the number that is expected to pay with a credit card would be;
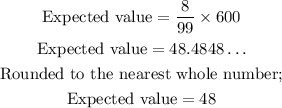
ANSWER:
About 48 customers would be expected to pay with a credit card