Question

Find the constants a and b that maximize the value ofb(9 − x2) dx.a

Answer 1

Answer: The function f is nonnegative between x=-3 and x=3

Given:

`\int_a^b(9-x^2)dx`

The given integral is also equal to the area between the curve of f(x)=9-x². To find the x-values that will maximize the value of the given, we could equate 9-x² to 0 and solve for x:

`\begin{gathered} 9-x^2=0 \\ x^2=9 \\ x=\pm3 \end{gathered}`

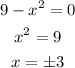
Checking the graph:

With these, we can say that the function f is nonnegative between x=-3 and x=3