Question

The sum of the lengths of any two sides of a triangle must be greater than the third side. If a triangle has one side that is 16 cm and a second side that is 2 cm less than twice the third side, what are the possible lengths for the second and third sides?

Answer 1

We are given that the sum of the lengths of any two sides of a triangle must be greater than the third side

To find the possible lengths for the second and third sides, we will make an assumption below.

Let the third side be x

Since the second side is 2 cm less than twice the third side, this can be expressed as

`\text{side 2=2x-2}`

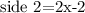
With this we can note that

side 1 = 16cm

side 2 =2x-2

side 3 = x

Going back to the initial rule that the sum of the lengths of any two sides of a triangle must be greater than the third side

We can sum any two sides and equate it to the third side.

`\begin{gathered} \text{side}2+\text{side}3\text{ >side1} \\ 2x-2+x>16 \\ 3x>16+2 \\ 3x>18 \\ x>(18)/(3) \\ x>6 \end{gathered}`

Since the third side is x therefore, the possible length of the third side is 6cm and above

ANSWER 1: third side= 7cm and above

Also, the second side is 2x-2. We will use a minimum value of 6

`\begin{gathered} \text{side 2 = 2x-2} \\ \text{side 2 = 2(}6\text{)}-2 \\ \text{side 2 =12-2} \\ \text{side 2 =10} \\ \\ \end{gathered}`

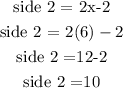
ANSWER 2: the second side is 10cm and above