The Law of Sines says that in any given triangle, the ratio of any side length to the sine of its opposite angle is the same for all three sides of the triangle. This is true for any triangle, not just right triangles.
In other words, the measure of an interior angle reflects the possible measure of the opposite side. The larger the measure of the angle, the larger the opposite side shoulde be.
In the given figure, it is shown that Side AB and BC are congruent. This should also mean that the opposite angles A and C should also be congruent.
Since it is also given that the measure of ∠C is 48°, the measure of ∠A should also be equal to 48°.

Recall that the sum of all interior angles of a triangle is 180°.
With this much details, we can now determine the measure of ∠B.
We get,

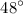



Therefore, the measure of ∠B is 84°.
The answer is CHOICE B.