Question

What is the process between the second and third step? I don’t get how step 3 has 10^2 power.

Answer 1

Base raised to logarithm rule

Step-by-step explanation

Between the second and third steps, a property of logarithms was applied, the base raised to logarithm rule. This property states that when the base of the logarithm is raised to the logarithmic expression, the result is the argument,

`a^(\log_a(x))=x`

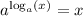
In this case, we can see that it only says "log", so we can assume that the base of this logarithm is 10. To get from step 2 to step 3, we have to raise the base (10) to each side of the equation,

`10^{\log((x+2)/(x+1))}=10^2`

And then, by the property stated above, we have the third line of this solution,

`(x+2)/(x+1)=10^2`

In the picture, the equation is inverted, but since there is an equal sign it is equivalent.