Question

Values for relation g are given in the table. Which ordered pair is in g inverse?

Answer 1

A scalar function is defined as:

'A function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.'

Therefore, if we have the following function

`f(x)=y`

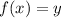
Given the x, y is unique.

The inverse function, takes the function value to its corresponding x value.

`f^(-1)(f(x))=f^(-1)(y)=x`

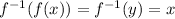
In our problem, we have the following function values

`\begin{gathered} g(5)=-3 \\ g(4)=1 \\ g(3)=-2 \\ g(2)=0 \end{gathered}`

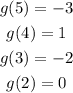
If we apply the inverse function on all of those values, we should get the argument of the function back.

`\begin{gathered} g^(-1)(g(5))=g^(-1)(-3)=5 \\ g^(-1)(g(4))=g^(-1)(1)=4 \\ g^(-1)(g(3))=g^(-1)(-2)=3 \\ g^(-1)(2)=g^(-1)(0)=2 \end{gathered}`

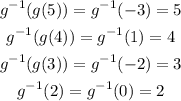
Therefore, from the possible answers, only (1, 4) belongs to the inverse.