Question

A stadium has a seating capacity of 1000. When the ticket price is $30 attendance is 400. For each $1 decrease in price attendance increases by 50. a) What is the number of $1 decreases in price that will maximize the revenue? b) What price per ticket will maximize the revenue? c) What is the maximum revenue?

Answer 1

Revenue: (30 + t)( 400 - 50t)

Attendance: 400 - 50t

a). $11 decrease in price maximises the revenue

b). $19 per ticket

c). $18,050

Step-by-step explanation:

We know that when we decrease the price by $1, the attendance increases by 50. Therefore, if we decrease our price n times, then the attendence becomes

`400+50n`

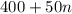
The price of the ticket then will have become

`30-n`

The revenue then will be

Revenue = attendence x price per ticket

`R=(400+50n)(30-n)`

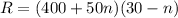
Now, the expression on the right-hand side is a parabola. The plot is given below.

As can be seen, the vertex of the parabola is (11, 18050).

a. The vertex tells us that if we decrease our ticket price by $11, then the revenue will be maximum.

b. The price per ticket that maximises the revenue is $30 - $11 = $19

c. As can be seen from the graph, the maximum revenue is $18050.

Hence, to summerise

a). $11 decrease in price maximises the revenue

b). $19 per ticket

c). $18,050