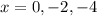Question

`f(x) = x ^(3) + 6x ^(2) + 8x`find the zeros. is itx= 0,-2,-4x= 0,2,4x= 2,4x= -2,-4

Answer 1

Given the function:

`f(x)=x^3+6x^2+8x`

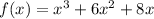
Let's find the zeros of the function.

To find the zeros of the function, take the following steps.

Step 1:

Set the function to zero

`x^3+6x^2+8x=0`

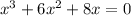
Step 2:

Factor the left side of the equation

Factor x out:

`x(x^2+6x+8)=0_{}`

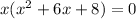
Now factor using the AC method:

`x(x+2)(x+4)=0`

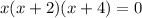
We have the factors:

x, x+2, x+4

Step 3:

Equate the individual factors to zero.

Thus, we have:

`\begin{gathered} x=0 \\ \\ x+2=0 \\ \\ x+4=0 \end{gathered}`

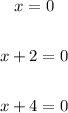
Step 4:

Solve each equation for x to get the zeros

• x = 0

• x + 2 = 0

Subtract 2 from both sides:

x + 2 - 2 = 0 - 2

x = -2

• x + 4 = 0

Subtract 4 from both sides:

x + 4 - 4 = 0 - 4

x = -4

Therefore, the zeros of the function are:

x = 0, -2, -4

ANSWER:

`x=0,-2,-4`